栏目导航
LDO的工作原理详细分析二
发表时间: 2024-12-27 05:22:34 作者: 贝博平台体育app官网
用包含三个极点和一个零点的波特图(图11:波特图)来分析增益和相位裕度。
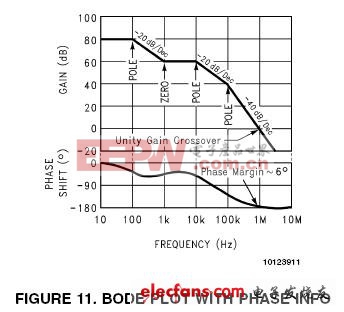
假设直流增益(DC gain)为80dB,第一个极点(pole)发生在100Hz处。在此频率,增益曲线kHz处的零点使斜度变为0dB/十倍频程,到10kHz处斜度又变成-20dB/十倍频程。在100kHz处的第三个也是最后一个极点将斜度最终变为-40dB/十倍频程。
相位偏移图表示了零、极点的不同分布对反馈信号的影响。为了产生这个图,就要依据分布的零点、极点计算相移的总和。在任意频率(f)上的极点相移,可以通过下式计算获得: 极点相移 = -arctan(f/fp) (6)
在任意频率(f)上的零点相移,可以通过下式计算获得: 零点相移 = -arctan(f/fz) (7)
此回路稳定吗?为了回答这样的一个问题,我们根本无需复杂的计算,只必须了解到0dB时的相移(此例中是1MHz)。
前两个极点和第一个零点分布使相位从-180°变到+90°,最后导致网络相位转变到-90°。最后一个极点在十倍频程中出现了0dB点。代入零点相移公式,可以计算出该极点产生了-84°的相移(在1MHz时)。加上原来的-90°相移,全部的相移是-174°(也就是说相位裕度是6°)。由此得出结论,该回路不能保持稳定,可能会引起振荡。
NPN 稳压器的导通管(见图1)的连接方式是共集电极的方式。所有共集电极电路的一个重要特性就是低输出阻抗,意味着电源范围内的极点出现在回路增益曲线的高频部分。
由于NPN稳压器没有固有的低频极点,所以它使用了一种称为主极点补偿(dominant pole compensation)的技术。方法是,在稳压器的内部集成了一个电容,该电容在环路增益的低频端添加了一个极点(图12:NPN稳压器的波特图)。
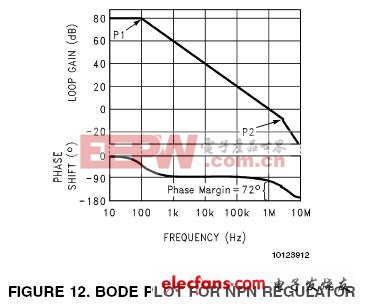
NPN稳压器的主极点(Dominant Pole), 用P1点表示, 一般设置在100Hz处。100Hz处的极点将增益减小为-20dB/十倍频程直到3MHz处的第二个极点(P2)。在P2处,增益曲线点的频率主要根据 NPN 功率管及相关驱动电路, 因此有时也称此点为功率极点(Ppower pole)。另外,P2点在回路增益为-10dB处出现,也就表示了单位增益(0dB)频率处(1MHz)的相位偏移会很小。
第一个极点(P1)会产生-90°的相位偏移,但是第二个极点(P2)只增加了-18°的相位偏移(1MHz处)。也就是说0dB点处的相位偏移为-108°,相位裕度为72°,表明回路非常稳定。
需要两个极点才有机会使回路要达到-180°的相位偏移(不稳定点),而极点P2又处于高频,它在0dB处的相位偏移就很小了。
LDO稳压器中的PNP导通管的接法为共射方式(common emitter)。它相对共集电极方式有更高的输出阻抗。由于负载阻抗和输出容抗的影响在低频程处会出现低频极点(low-frequency pole)。此极点,又称负载极点(load pole),用Pl表示。负载极点的频率由下式计算获得:
从此式可知,LDO不能通过简单的添加主极点的方式实现补偿。为什么? 先假设一个5V/50mA的LDO稳压器有下面的条件,在最大负载电流时,负载极点(Pl)出现的频率为:
假设内部的补偿在1kHz处添加了一个极点。由于PNP功率管和驱动电路的存在,在500kHz处会出现一个功率极点(Ppwr)。
假设直流增益为80dB。在最大输出电流时的负载阻值为RL=100Ω,输出电容为Cout =10uF。
使用上述条件可以画出相应的波特图(如图13:未补偿的LDO增益波特图)。
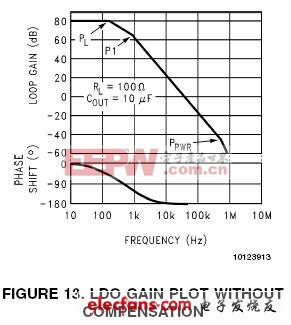
可以看出回路是不稳定的。极点PL和P1每个都会产生-90°的相移。在0dB处(此例为40kHz),相移达到了-180°为减少负相移(阻止振荡),在回路中必须要添加一个零点。一个零点可以产生+90°的相移,它会抵消两个低频极点的部分影响。
因此,几乎所有的LDO都需要在回路中添加这个零点。该零点一般是通过输出电容的等效串联电阻(ESR)获得的。
等效串联电阻(ESR)是电容的一个基本特性。可以将电容表示为电阻与电容的串联等效电路(图14:电容器的等效电路图)。

输出电容的ESR在回路增益中产生一个零点,可拿来减少负相移。零点处的频率值(Fzero)与ESR和输出电容值密切相关:
再看上一节的例子(图13),假设输出电容值Cout =10uF,输出电容的ESR = 1Ω。则零点发生在16kHz。图15的波特图显示了添加此零点如何使不稳定的系统恢复稳定。
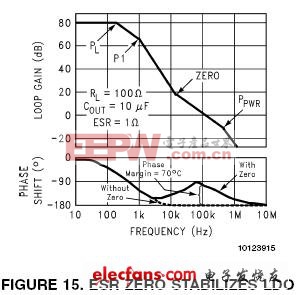
回路的带宽增加了,单位增益(0dB)的交点频率从30kHz移到了100kHz。到100kHz处该零点总共增加了+81°相移(Positive Phase Shift)。也就是减少了极点PL和P1造成的负相移(Negative Phase Shift)。 极点Ppwr处在500kHz,在100kHz处它仅增加了-11°的相移。累加所有的零、极点,0dB处的总相移为-110°。也就是有+70°的相位裕度,系统非常稳定。
通常所有的LDO都会要求其输出电容的ESR值在某一特定范围内,以保证输出的稳定性。 LDO制造商会提供一系列由输出电容ESR和负载电流(Load Current)组成的定义稳定范围的曲线:典型LDO的ESR稳定范围曲线),作为选择电容时的参考。
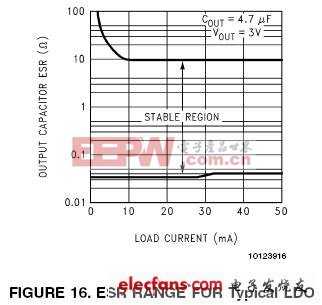
要解释为什么有这些范围的存在,个人会使用前面提到的例子来说明ESR的高低对相位裕度的影响。
同样使用上一节提到的例子,我们假设10uF输出电容的ESR增加到20Ω。这将使零点的频率降低到800Hz(图17:高ESR引起回路振荡的波特图)。
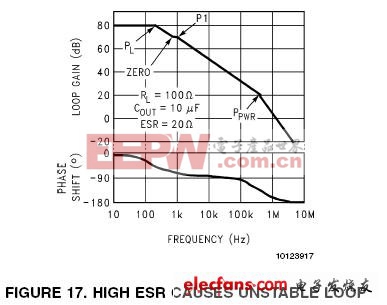
降低零点的频率会使回路的带宽增加,它的单位增益(0Db)的交点频率从100kHz 提高到2MHz。 带宽的增加意味着极点 Ppwr 会出现在带宽内(对比图15)。分析图17波特图中曲线的相位裕度,发现如果同时拿掉该零点和P1或PL中的一个极点,对曲线的形状影响很小。也就是说该回路受到-90° 相移的低频极点和发生-76° 相移的高频极点Ppwr共同影响。
尽管有 14° 的相位裕度,系统可能会稳定。但很多经验测试多个方面数据显示,当ESR >10Ω时,由于其它的高频极点的分布(在此简单模型中未表示)非常有可能会引入不稳定性。
选择具有很低的ESR的输出电容,由于一些不同的原因也会产生振荡。继续沿用上一节的例子,假定10uF输出电容的ESR只有50mΩ,则零点的频率会变到320kHz(图18:低ESR引起回路振荡的波特图)。
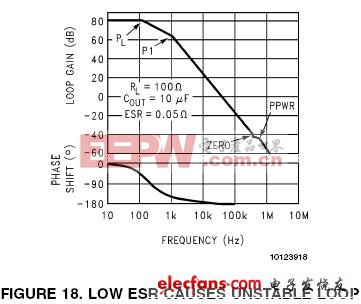
不用计算就知道系统是不稳定的。两个极点P1和PL在0dB处共产生了-180°的相移。如果要系统稳定,则零点应该在0dB点之前补偿正相移。然而,零点在320kHz处,已经在系统带宽之外了,所以没办法起到补偿作用。
- 上一个: 蓝景 LJ-ICP7800:科研检测的得力助手
- 下一个: 新界泵业获得一种稳压设备及补偿设备专利





